Topic = 시간 복잡도를 학습해야 하는 이유, 시간복잡도의 개념, 활용 등에 대해서 학습해보자
Why - 시간 복잡도를 배우기 전에 함께 알아본 것 ( 상위 개념, 학습하는 이유 )
상위 개념 - 계산 복잡도 이론
☑️ ( 일련의 과정을 자원 측정 및 분류, 구성된 모임의 복잡도 확인, 점근적 표현 )
- ➡️ 아래에서 시간 복잡도 계산시 해당 단계를 활용하여 다룰 것.
계산 복잡도 이론은 알고리즘이 일련의 문제를 해결하는데 필요한 자원을 측정하고 분류하는 이론으로, 알고리즘을 복잡도에 따른 데이터 구조의 모임을 구성하고 알고리즘이 소모하는 시간과 메모리 사용량 등의 자원을 효율성 지표로 사용하는 것이다. 이 효율성 지표중, 소모하는 시간의 효율성 지표를 시간 복잡도, 메모리 사용량의 지표를 공간복잡도라고 하며 점근적으로 표현한다.
계산 복잡도를 학습 해야 하는 이유
- 효율성을 평가하며 알고리즘 설계가 용이
- 알고리즘이 해결하려는 문제의 크기가 커질 때, 얼마나 잘 확장되는지 등의 자원의 효율성을 비교 해볼 수 있다.
- 대량의 데이터를 처리할 때, 데이터 정렬에 사용되는 다양한 알고리즘 방식 ( 버블 정렬, 퀵 정렬, 병합 정렬 등 ) 의 복잡도를 계산해보고, 어떤 알고리즘이 적합할지 평가할 수 있다.
즉, 시간 복잡도와 공간 복잡도는 다양한 솔루션의 성능과 리소스 사용량의 효율성을 평가하여 알고리즘을 개선 및 설계 등의 지표로 사용될 수 있다.
점근적 표기법
- 완료까지 필요한 ' 시간 ' 은 각 컴퓨터 ( 하드웨어 ) 의 성능에 따라 다르기 때문에, 모든 하드웨어가 동일하게 적용될 수 있는 완료까지의 필요한 절차수를 표기하는 방식이다.
- 입력 데이터의 크기가 커짐에 따른 성능의 변화에 영향을 받지 않는 중요하지 않은 항과 상수, 계수 항목을 제거하여 표기하는 방법으로, 알고리즘의 입력 데이터에 따른 실행 시간의 성장률에 집중한다.
점근적 표기법 3가지 방식들 ( 빅오메가, 빅오, 빅세타 표기법 )
[ 빅오메가 표기법 - Ω(1) ➡️ lower bound ( 하한선 ) ] 😿 거의 사용 X
완료까지의 필요한 절차수가 얼마나 커질지는 모르겠지만, 최소 Ω(1) 만큼의 절차가 필요하다는 의미의 점근적 표기법 형태이다.
[ 선형 탐색 시 Bset Case 예시, 한번에 찾으려면 찾을 수 있으니, Ω ( 1 ) ]

[ 빅오 표기법 - O(N) ➡️ upper bound ( 상한선 ) ]
🟥 시간복잡도를 표현할 때, 일반적으로 빅오 표기법을 사용한다.
빅오( O(n) ) 표기법은 인자가 특정한 값 이상의 무한대로 향할 때 극학적인 동작을 설명하는 표기법으로, 시간 복잡도에서는 n이 무한대로 커질때 실행시간이 O(n) 이하로 실행될 것이라는 것을 표현하는 것이다.
[ n의 상승률에 따른 Wosrt case 예시로, Worst Case ➡️ O(n) 을 나타냄 ]

선형 검색의 경우의 예시를 들었을 때, 아래 사진과 같이 0 부터 10까지 요소가 랜덤하게 위치해 있다고 가정해보자. Index 0부터 끝까지의 순서대로 값을 확인하는 방법 으로 접근하게 된다고 하면, 찾으려고 하는 값이 5던 10이던 배열의 갯수인 10번 안에는 끝나게 된다. 이처럼 실행 시간이 아무리 오래 걸려도 이정도까지만 걸린다. 라는 것을 표현하는 것이 빅오 표기법 - O(n)이다.

❓왜 빅오 표기법을 많이 쓸까
1. 최대 경우의 수인 upper bound만 있어도, 시간 복잡도에 예외가 없다
- 이진 검색의 경우에 θ(log2N) 시간안에 실행된다고 할 수 있지만 항상 θ(log2N) 시간에 실행되는 것은 아니다.
- 이진 검색 실행 시간의 최악의 경우는 θ(log2N) 이지만 O(log2n) 으로도 표현이 가능하다.
2. 최악의 경우를 표기함으로 성능을 보수적으로 평가할 수 있다.
- 입력 데이터가 클 최악의 경우의 성능이 시스템 전체에 미치는 영향이 매우 크기 때문에 보수적인 평가가 중요하다.
➡️2번 이유에 예시를 들어보자.
솔루션을 사용하는 사용자들의 사용 데이터에 따라 적용되는 2개의 알고리즘을 설계하였다.
A. A알고리즘은 최소한 전체 사용자의 데이터량을 logN 확인해야 원하는 값을 확인할 수 있고 최대 N번에 확인할 수 있다.
B. B알고리즘은 잘하면 1번의 경우에 찾을 수 있지만, 최대 N^2 번에 확인할 수 있다.
A 의 시간 복잡도 → Ω(logN) or O(N)
B 의 시간 복잡도 → Ω(1) or O(n^2)
위 알고리즘을 선택할 때 빅오메가 (최소 실행시간 - lower bound) 기준으로 선택하여 B의 알고리즘을 선택하게 될 경우.
일반적인 사용자들이 100의 사용 데이터를 가지고, 단골 사용자들은 5만의 사용 데이터를 가지는 상황에서 각각의 사용자에게 운이 좋으면 1번의 실행에 함수가 종료될 수도 있지만. 최악의 경우 50,000^2 의 실행 시간이 걸릴 수 있으므로 최선의 경우를 바탕으로 알고리즘을 선택하는 방법은 좋지 않은 선택이 되기 쉽다.
[ 시간 복잡도 속도 비교표 ]
왼쪽부터 실행시간이 빠른 순서로 오른쪽으로 갈수록 실행 시간이 큰 함수이다.
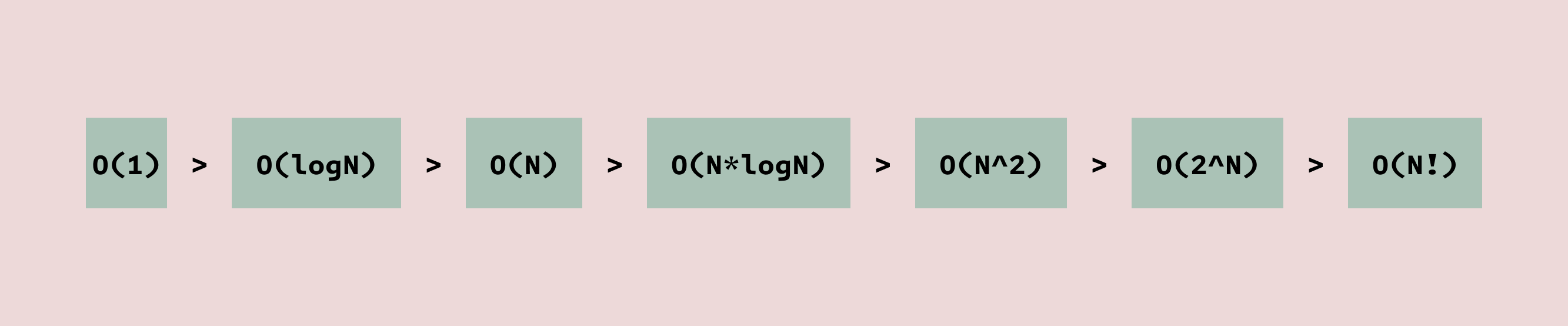
[ 빅세타 표기법 - θ(n) ➡️ tight bound ]
🟪 알고리즘에서 어떤 상수 n의 배수 내에서 lower와 upper bound ( 최선, 최악의 경우) 가 근사할 때 ( = tight bound)
- 빅세타 표기법은 알고리즘의 실행 시간이 상황과 하한에 의해 동일한 주요 항으로 근사될 수 있을 때, 즉 최선의 경우와 최악의 경우가 근사한 차수임을 표현할 때 사용된다.
- 🟨 선형 탐색의 상황을 예시로 들어보면, 배열의 길이가 100일 때, 최선의 경우의 시간은1이고 최악의 경우 (찾는 값이 마지막에 있거나, 없을 때 )는 100의 시간이 필요하다. 선형 탐색의 접근에서는 평균적으로 반정도는 검사한다 라는 의미에서 빅세타 표기법으로, 평균적인 시간 복잡도를 θ(2/1n) 으로 볼 수 있다. 점근 표기에서는 상수와 계수를 없애기 때문에 O(n) 과 마찬가지로 θ(n) 으로 표현된다. n의 크기가 커짐에 비례해서 시간이 증가된다는 것은 맞지만, 선형탐색의 경우 단순히 θ(n) 으로 표현하기보다 O(n) 으로 표현하는 것이 적합한 느낌이다.
- 🟪 에서는 lower, upper bound 가 근사할 때라고 했는데, 🟨 의 예시인 선형 탐색의 경우에도 빅세타 표기법이 가능하기는 하다. 근데 🟨 의 설명에서 봤듯이, lower bound와 upper bound가 같지 않은 상황에서 빅세타 표기법을 사용하게 되면, 모든 실행 경우의 100% 만족하는 표현이 아니게 된다. 때문에 세타 표기법은 알고리즘에서 어떤 상수 배수 내에서 최선, 최악의 경우가 양방향으로 제한되어 근사할 때 사용하는 것이 권장된다.
[ 최선, 최악의 케이스로 양방향이 제한된 상승률 예시 ]
시간 복잡도
함수의 실행 시간을 점근적 분석을 통해 실행시간을 점근적 표기법으로 표현하는 것.
[ 시간복잡도 계산 과정 예시 ]
fun test (a: IntArray, b: IntArray): Int {
var arrSize = a.size // 1
for (i in 0..arrSize) { // a + 1
println("a")
}
for (i in 0..a.size) { // a + 1
println("a2")
}
for (i in 0..b.size) { // b + 1
println("b")
}
return a.size + b.size // 1
}위와 같은 함수가 있을 때 시간 복잡도를 구하는 과정은 아래와 같다.
1. 분류
- 알고리즘 내부 일련의 작업들의 자원을 측정 및 분류한다. test 함수 예시를 들면 변수 arrSize 가 a.size의 값으로 할당되는 것은 test 함수가 진행될 때 1번만 실행되므로 1, for문 안에 0 .. arrSize 는 a.size + 1 번 반복 되므로 a + 1 이고 b 반복문도 b + 1 번 반복된다
2. 구성된 모임의 복잡도 확인
- 1에서 분류한 각각의 일련의 작업들에 소모되는 자원을 ( 복잡도 ) 를 확인한다.
- 일련의 과정들의 모임의 자원 ➡️ 1 + 2a + 2 + b + 1 + 1
- ∴ 2(a.size) + b.size + 5
3. 점근적으로 표현
- 불필요한 항과, 계수, 상수를 제거하여 표기
- 상수 및 계수는 상승률에 영향을 주지 않기 때문에 제거.
- ∴ O(n + m) test 함수의 시간 복잡도는 O(n+m)이 된다.
[ 시간복잡도 활용 예시 - 이분탐색/이진탐색 ]
대기표 번호 순서대로 입장이 가능한 디저트 맛집에서 특정 대기자가 자신의 입장순서가 얼마나 남았는지 확인할 수 있도록 하려고 함수를 작성할 때, 간단하게 아래와 같이간단한 코드로 작성할 수 있다.
private fun testFun ( n : IntArray , target : Int ) : Int {
return n.indexOf(target)+1
}- indexOf ( 선형탐색 ) 으로 target의 대기표 번호가 600일때,현재 대기열인 n의 배열이 [400, 401, 402, ... 601 ] 일 경우, 400부터 598, 599, 600 으로 배열 전체를 확인하기 때문에 O(n) 의 시간 복잡도를 갖는다.
- 사전에서 단어를 검색할 때, ' 탐색 ' 이라는 단어를 찾으려고 할 때, ㄱ,ㄴ,ㄷ,ㄹ ... 모든 단어를 찾게 된다면 시간이 더 소요되게 되기에 페이지를 폈을때 자음이 ㄹ이면 뒷 페이지로, 자음이 ㅎ이면 앞 페이지로 이동할 것이다. 이를 이분 탐색 법이라고 한다.
위 코드에 이분탐색 알고리즘을 적용할 경우의 시간복잡도를 확인 해보자.
fun testFun2(n: IntArray, target: Int): Int {
var left = 0
var right = n.size - 1
while (left <= right) {
val mid = left + (right - left) / 2
val midValue = n[mid]
when {
midValue == target -> return mid + 1
midValue < target -> left = mid + 1
else -> right = mid - 1
}
}
return -1
}n이 [ 400 .. 600 ] 의 배열일 때, 500 부터 시작해서 타겟까지의 찾을 목록들을 반으로 줄여서 접근하므로, n배열의 모든 값에 접근하지 않아도 target을 찾을 수 있게 된다.
O(logN) 의 시간 복잡도로 기존 코드의 시간 복잡도인 O(n) 보다 복잡도가 낮은 ( 효율성이 높은 ) 코드로 작성이 가능하다.
🚧 TODO 더 자세한 시간 복잡도 활용 방법 등을 학습 후 [ 시간 복잡도 2. 활용 방법 ] 작성 후 링크 추가

[ A. 오늘 복습한 내용 / B. 다음에 학습할 내용 ]
A. 특별한 복습 내용 X
B. 공간 복잡도
B. 버블정렬, 퀵정렬 등의 정렬 방식들
[오류,에러 등등]
1. 어떤 자료에서 아래와 같은 상황에 θ(N+M) 를 θ(max(n,m)) 와 같이 사용할 수도 있다고 하는데 이해가 잘 되질 않음.

[느낀 점]
1. 개념 자체를 학습하면서는 재밌게 학습했던 개념인데, 시간 복잡도를 활용하여 여러 정렬 알고리즘에 적용해서 비교하는 부분은 아직 알고리즘 정렬 방식을 학습하지 않아서 시도해보지 못했다. 추후 학습 예정.
2. 개념 학습은 늘 재미있으면서도 막막한 느낌이다. 😿
[Reference]
시간 복잡도 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 러닝 타임은 여기로 연결됩니다. 매체의 재생·상영 시간에 대해서는 러닝 타임 (매체) 문서를 참고하십시오. 계산 복잡도 이론에서 시간 복잡도는 문제를 해결
ko.wikipedia.org
시간복잡도 개념, Big-O(빅 오) 표기법, 점근적 표기법 설명
영상 내용을 글로도 정리했습니다 아주 아주 쉽게 설명합니다 :) 예제로 알아보는 시간 복잡도(time complexity) 개념 아래와 같은 코드가 있습니다. 이 코드는 정수 타입의 배열 inputs과 multiplier를 파
easy-code-yo.tistory.com
'CS' 카테고리의 다른 글
| [CS] 정렬 알고리즘 - 기본개념 [ 버블 정렬, 선택 정렬, 삽입 정렬, 힙 정렬, 병합 정렬, 퀵 정렬 ] (0) | 2024.05.21 |
|---|---|
| [CS] 프로그램 ( Program ), 프로세스 ( Process ), 쓰레드 ( Thread ) 학습 - 작성중 (1) | 2024.04.30 |
| [TIL] Kotlin - 재귀 함수, 꼬리재귀 ( Tailrec ) 함수 (1) | 2024.04.20 |


